Maximum cut and related problems
In this lecture, we will discuss three fundamental NP-hard optimization problems that turn out to be intimately related to each other. The first is the problem of finding a maximum cut in a graph. This problem is among the most basic NP-hard problems. It was among the first problems shown to be NP-hard (Karp 1972).This problem also shows that small syntactic changes in the problem definition can make a big difference for its computational complexity. The problem of finding the minimum cut in a graph has a polynomial-time algorithm, whereas a polynomial-time algorithm for finding a maximum cut is unlikely because it would imply P=NP. The second problem is estimating the expansionIn the literature, several different terms, e.g., expansion, conductance, and sparsest-cut value, are used to describe closely related parameter of graphs. In these notes, we will not distinguish between these parameters and stick to the term expansion. of a graph. This problem is related to isoperimetric questions in geometry, the study of manifolds, and a famous inequality by Cheeger (1970). The third problem is estimating mixed norms of linear operators. This problem is more abstract than the previous ones but also more versatile. It is closely related to a famous inequality by Grothendieck (1953).
How are these seemingly different problems related? First, it turns out that all three of them can be phrased in terms of optimizing a quadratic polynomial over the hypercube. Second, all three have beautiful approximation algorithms based on degree-2 sum-of-squares which give the bestfor a suitable notion of “best” known guarantees for the respective problem.One interesting feature of these algorithms also is that we don’t know how to achieve the same approximation guarantees with different algorithmic techniques. In this sense, sum-of-squares brings something unique to the table for these problems. Third, any improvement in the approximation guarantee of these algorithms would refute the Unique Games Conjecture (Khot 2002) or the closely related Small-Set Expansion Hypothesis (Raghavendra and Steurer 2010).
Approximating the maximum cut
We now define the Max Cut problem:
Given a graph, find a bipartition of the vertex set that cuts as many edges as possible.
For every graph \(G\), we let \({\mathrm{maxcut}}(G)\) denote the fraction of edge cut by an optimal Max Cut solution for \(G\). Max cut is a natural graph problem, motivated by applications such as efficient design of electric circuits or communication networks, but has also found uses to questions in statistical physics such as finding an energy minimizing configuration in the ising model.For more applications, see also the survey (Deza and Laurent 1994). But more than this, the Max Cut problem has served as a prototypical testbed for algorithmic techniques that have found extensive and sometimes surprising applications. For example, a variant of the algorithm for Max Cut that we present in this lecture has been used for the Phase Retrieval problem that appears in X-ray crystallography, diffraction imaging, astronomical imaging and other applications (see (Candès et al. 2013; Waldspurger, d’Aspremont, and Mallat 2015)).
Since a random bipartition cuts half the edges in expectation, there is an efficient randomizedIf you haven’t encountered randomized algorithms before, it’s a useful exercise to convince yourself that this algorithm can be derandomized: Show that there exists an efficient deterministic algorithm that given an undirected graph outputs a bipartition that cuts at least half of the edges. algorithm to find a bipartition that cuts at least \(\tfrac 12 \cdot {\mathrm{maxcut}}(G)\) of the edges. We say that this algorithm achieves an approximation factor of \(\tfrac 12\). In fact, this algorithm for Max Cut was suggested by Erdős in 1967, and is one of the first analyses of any approximation algorithm.
A priori, it is not clear how to beat this approximation ratio or if that is possible at all. In a random \(d\)-regular graph (which is an excellent expander), one cannot cut more than a \(\tfrac12 + \e\) fraction of the edges (where \(\e\) goes to zero as \(d\) goes to infinity). But locally, it is hard to distinguish a random \(d\)-regular graph from a random \(d\)-regular “almost bipartite” graph, where we split the vertex sets into two parts of equal size and each edge is with probability \(\e\) inside one of those parts and with probability \(1-\e\) between them. Such a graph \(G\) obviously has \({\mathrm{maxcut}}(G)\geq 1-\e\) but every neighborhood of it looks like a \(d\)-regular tree, just as in the case of a random \(d\)-regular graph. For this reason, “combinatorial” (or even linear programming) algorithms have a hard time getting an approximation factor better than \(\tfrac12\) for Max Cut. Indeed, Chan et al. (2013) show that no linear programming relaxation of polynomial-size can have an approximation factor smaller than \(\tfrac12\) factor for Max Cut.
As alluded to before, sum-of-squares techniques allow us to go beyond approximation factor \(\tfrac 12\) for Max Cut (Goemans and Williamson 1994).
There exists a polynomial time algorithm that given a graph, outputs a bipartition such that the number of cut edges is at least \(0.878\) times the maximum number possible.
Max cut as a quadratic optimization problem over the hypercube
In order to apply the sum-of-squares framework we formulate Max Cut as a polynomial optimization problem. Let \(G\) be a graph of \(n\) vertices. Identify the vertex set of \(G\) with \([n]\). We let a vector \(x\in \bits^n\) represent the bipartition of \([n]\) such that one side consists of every vertex \(i\) with \(x_i=1\). Let \(f_G\) be the function that assigns to every \(x\in \bits^n\) the number \(f_G(x)\) of edges cut by the bipartition that \(x\) represents. Then, \(f_G\) agrees with the following quadratic polynomial for every \(x\in\bits^n\), \[ f_G(x) = \sum_{(i,j)\in E(G)} (x_i - x_j)^2\,. \]
Thus the task of computing \({\mathrm{maxcut}}(G)\) is identical to the task of computing \(\max_{x\in\bits^n} f_G(x)\).In the previous lecture our focus was on minimizing a function over the cube. However note that maximizing a function \(f\) is equivalent to minimizing \(-f\), and hence we will freely use whichever formulation is more natural for a given problem.
Sum-of-squares certificates for Max Cut
A simple way to describe the power of sum-of-squares for Max Cut is in terms of certificates. In order to certify that some graph \(G\) and some value \(c\) satisfy \(\max f_G \ge c\) it is enough to exhibit a single bipartition \(x\in\bits^n\) of \(G\) such that \(f_G(x)\ge c\). In contrast, it is unclear how to efficiently certify statements of the \(\max f_G \le c\) because any certificate has to rule out an exponential number of possible bipartitions \(x\). The following theorem shows that sum-of-squares provides efficient certificates for the inequality \(f_G \le c\) as long as \(c\ge \max f_G / 0.878\).
For every graph \(G\) with \(n\) vertices, there exist linear functions \(g_1,\ldots,g_n \from \bits^n\to \R\) such that for every \(x\in \bits^n\), \[ \max (f_G) - 0.878\cdot f_G(x) = g_1(x)^2 + \cdots + g_n(x)^2\,. \]
The rest of this section is devoted to proving Reference:max-cut-approximation and Reference:degree-2-sos-certificates-for-max-cut.
Aside: sum-of-squares certificates and eigenvalues
There is a fairly straightforward way to certify some non-trivial bound on the maximum cut. For a graph \(d\)-regular \(G\) with vertex set \([n]\) and edge set \(E\), let \(A=A(G)\) be its adjacency matrix of \(G\), i.e.,s the \(n\)-by-\(n\) matrix \[ A_{i,j} =\begin{cases} 1 & \text{if $\set{i,j}\in E$},\\ 0 & \text{otherwise.} \end{cases} \] Let \(\lambda\) be the smallest eigenvalue (i.e., most negative) of \(A\). Note that \(\lambda\) is in \([-d,0)\) (can you see why?) and, as you will show in the exercise below, \(\lambda=-d\) if and only if \(G\) contains a bipartite connected component. Now, for every bipartition \(x\in\bits^n\) corresponding to some set \(S\subseteq [n]\), if \(y\in \sbits^n\) is the vector \(y=1-2x\) then \(y^t A y = 2(|E(S,S)|+|E(V\setminus S)|) - 2|E(S,V\setminus S)|=2|E|-4|E(S,V\setminus S)|\).The edges inside \(S\) and \(V\setminus S\) get counted with a positive sign and the ones between \(S\) and its complement get counted with a negative sign. The factor of two is because every edge is counted twice. Hence, since \(y^\top A y \geq \lambda \norm{y}^2 = \lambda n\), we get that \(|E(S,V\setminus S)| \leq |E|/2-n\lambda/4\). In particular, since \(|E|=nd/2\), if \(\lambda \geq -(1-\epsilon)d\) we get that \(|E(S,V\setminus S)|\leq (1-\epsilon/2)|E|\).
The exercises below ask you to show that this bound can in fact be proven via a sum-of-squares proof and moreover that this bound is non-trivial (i.e., smaller than \(|E|\)) for every non-bipratite graph. (The first exercise is closely related to this exercise in the notes for lecture 1).
Let \(G\) be a \(d\)-regular graph with \(n\) vertices. Suppose the adjacency matrix of \(G\) has smallest eigenvalue \(\lambda\). Show that for \(c = \tfrac 12 \cdot (1-\lambda/d)\) the function \(c\cdot \card{E} - f_G\) has a degree-2 sos certificate.This certificate shows that \({\mathrm{maxcut}}(G) \le c\)
Prove that for every \(d\)-regular connected non-bipartite graph \(G\), the minimum eigenvalue of \(A(G)\) is larger than \(-d\).
Show that for every \(\epsilon>0\) there exists some \(d\) and a \(d\) regular connected graph \(G\) such that \({\mathrm{maxcut}}(G)\leq 1/2 + \epsilon\) but the minimum eigenvalue of \(G\) is at most \(-(1-\epsilon)d\).
Show that for a random \(d\)-regular graph the eigenvalue bound certifies that \({\mathrm{maxcut}}(G)\le 1/2+o(1)\), where \(o(1)\) goes to \(0\) as \(d\) goes to infinity.
For more about the relationship between the minimum eigenvalue and the max cut value, see Trevisan (2009).
Pseudo-distributions for Max Cut
Recall the definition of pseudo-distribution over the hypercube. For functions \(\mu,f\from \bits^n\to \R\), we denote the pseudo-expectation of \(f\) under \(\mu\) as \[\pE_{\mu} f=\sum_{x\in \bits^n} \mu(x)\cdot f(x)\,.\] (We extend the above definition also to vector-valued functions \(f\).) We say that \(\mu\) is a degree-\(2k\) pseudo-distribution if \(\E_\mu 1 = 1\) and \(\E_\mu g^2\ge 0\) for all \(g\from \bits^n\to\R\) with \(\deg g\le k\).
By the duality between sos certificates and pseudo-distribution, the theorem below implies Reference:degree-2-sos-certificates-for-max-cut. Furthermore, since we can optimize over low-degree moments of pseudo-distributions over the hypercube up to arbitrary accuracy, the theorem below also implies Reference:max-cut-approximation.
For every graph \(G\) and degree-\(2\) pseudo-distribution \(\mu\) over the hypercube, there exists a probability distribution \(\mu'\) over the hypercube such that \[ \E_{\mu'} f_G \ge 0.878 \cdot \pE_{\mu} f_G\,. \] Furthermore, there exists a randomized polynomial-time algorithm that given the pseudo-distribution \(\mu\) (say represented by its degree-2 moments \(\E_{\mu(x)} \dyad x\)) outputs a sample from \(\mu'\).
Let \(\Ind\) denote the all-ones vector in \(\bits^n\). For simplicity, assume \(\pE_{\mu(x)} x= \tfrac 12 \cdot \Ind\). (Otherwise, consider the pseudo-distribution \(\tfrac 12 (\mu(x)+\mu(\Ind-x))\), which satisfies this property and has the same pseudo-expectation for \(f_G\).) We define the probability distribution \(\mu'(x')\) in terms of the following sampling algorithm:
- Choose \(\xi\) as a Gaussian vector with covariance \(\pE_{\mu(x)}\dyad x\) and mean \(\pE_{\mu(x)} x\) (see quadratic sampling lemma from lecture 1).
- Output \(x'\in \bits^n\) with \(x'_i = 0\) if \(\xi_i < \tfrac 12\) and \(x'_i=1\) otherwise.
By the form of \(f_G\), it is enough to show the following inequality for all \(i,j\in [n]\). \[ \E_{\mu'(x')} (x'_i-x'_j)^2 \ge 0.878 \cdot \pE_{\mu(x)} (x_i - x_j)^2\,. \] Fix the indices \(i\) and \(j\) in \([n]\). Since \(\mu\) is a pseudo-distribution over the hypercube, \(x_i\) and \(x_j\) have variance \(\pE_{\mu(x)} x_i^2 -\tfrac 14=\pE_{\mu(x)} x_j^2-\tfrac14 = \tfrac14\).This step is the only one that uses the fact that we are interested in the maximum value of \(f_G\) over the hypercube as opposed to the sphere. Let \(\rho=4\pE_{\mu(x)} x_i x_j -1\) be the covariance of \(x_i\) and \(x_j\) under \(\mu\) (after rescaling them to have variance \(1\)). Since \(\xi\) is Gaussian with the same first two moments as \(x\), \[ (\xi_i,\xi_j) \sim \cN\Paren{ \tfrac12\cdot \Paren{ \begin{smallmatrix} 1 \\ 1 \end{smallmatrix}}, \tfrac14\cdot \Paren{ \begin{smallmatrix} 1 & \rho \\ \rho & 1 \end{smallmatrix}}}\,. \] Therefore, \(2\xi_j-1=\rho \cdot (2\xi_i-1)+\sqrt{1-\rho^2}\cdot \xi_i^\bot\), where \(\xi_i^\bot\sim\cN(0,1)\) is a standard Gaussian independent of \(\xi_i\). It follows that \[ \begin{aligned} \E_{D'(x')} (x'_i-x'_j)^2 & = \Pr_{\xi_i,\xi_j} \Set{ \sign(2\xi_i-1)\neq \sign(2\xi_j-1)} \\ &= \Pr_{s,t\sim \cN(0,1)} \Set{ \sign s \neq \sign\Paren{\rho \cdot s + \sqrt{1-\rho^2\,} \cdot t}}\,. \end{aligned} \] The event on the right-hand side consists of the set of all pairs \((s,t)\) in two conic regions symmetric around the origin that each form an angle of \(\arccos \rho\). By rotational symmetry of the Gaussian distribution, it follows that the event has probability \(\frac{\arccos \rho}{\pi}\).
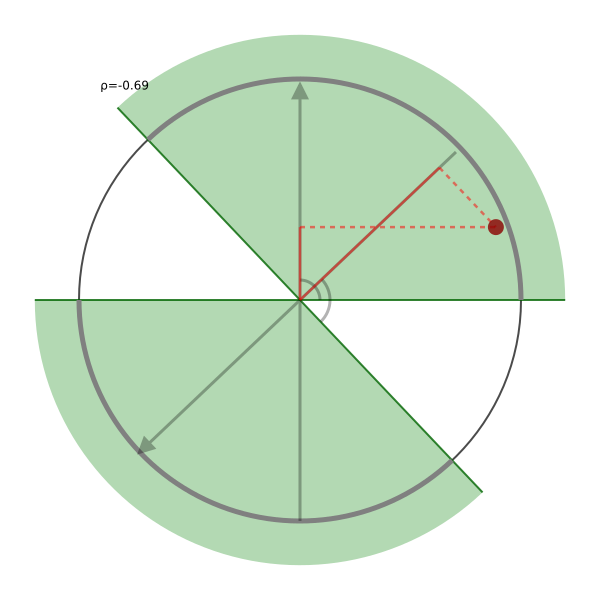
At the same time, \[ \E_{\mu(x)} (x_i - x_j)^2 = \tfrac 12 \cdot (1-\rho)\,. \] Therefore, it remains to verify that \[ \frac{2\arccos \rho}{(1-\rho)\pi} \ge 0.878\,, \] which we can do by single-variable calculus.
In the proof of Reference:rounding-pseudo-distributions-for-max-cut it may seem almost “accidental” that the final constant ends up being bigger than \(1/2\). However, if we just wanted to see that the approximation ratio is bigger than \(1/2\) a more direct calculation suffices. Note that if the optimal value \({\mathrm{maxcut}}(G)\) is smaller than say \(0.99\) then already the naive randomized algorithm achieves an approximation ratio of \(0.99/0.5\), which is bigger than \(1/2\). Therefore, the challenge is to find bipartitions for graphs with \({\mathrm{maxcut}}(G)\ge 0.99\) that cut significantly more than half of the edges. The following exercise gives a “calculus free” analysis of an algorithm with this property.
Show every degree-\(2\) pseudo-distribution \(\mu\) over the hypercube, there exists an efficiently sampleable probability distribution \(\mu'\) over the hypercube such that for every \(\e>0\) and every graph \(G\), \[ \pE_{\mu} f_G \ge (1-\e)\cdot \card{E(G)} \Longrightarrow \E_{\mu'} f_G \ge (1-2\sqrt \e)\cdot \card{E(Gs)}\,. \] (In particular, when \({\mathrm{maxcut}}(G)\ge 0.99\), we can take \(\e=0.01\) and get bipartitions with expected value at least \(1-2\cdot 0.1=0.8>0.5\) under \(\mu'\).)Hint: You can use the same construction for \(\mu'\) as in the proof of Reference:rounding-pseudo-distributions-for-max-cut.
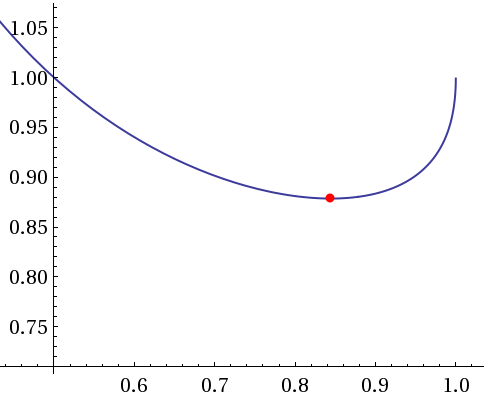
In general, we can ask about the curve between the value of the pseudo-distribution and the value achieved by a rounding algorithm. Concretely, for every value of \(c\), what is the largest value of \(s\) such that a degree-\(2\) pseudo-distribution with \(\pE_\mu f_G \ge c\cdot \card{E(G)}\) for a graph \(G\) always allows us to efficiently find a bipartition \(x\) with value \(f_G(x)\ge s\cdot \card{E(G)}\). It turns out that the above algorithm does not achieve the best possible “approximation curve” but similar ideas work, see (O’Donnell and Wu 2008).
The following exercise asks you to analyze the approximation curve of the Goemans–Williamson algorithm for a particular range of \(c\).
Let \(c_{\mathrm{GW}}\approx 0.845\) be the minimizer of \(c\mapsto\arccos(1-2c)/(\pi c)\) and let \(\alpha_{\mathrm{GW}} \approx 0.878\) be the minimum value of this function. Show that for every \(c \geq c_{\mathrm{GW}}\), every graph \(G\), and every degree-\(2\) distribution \(\mu\) over the hypercube such that \(\pE_\mu f_G = c\cdot|E|\), there is an actual distribution \(\mu'\) such that \(\pE_{\mu'} f_G \geq \arccos(1-2c)/\pi\).Hint: Prove first that the following function \(g:[0,1]\rightarrow\R\) is convex: \(g(c)=\alpha_{\mathrm{GW}}c\) for \(c<c_{\mathrm{GW}}\) and \(g(c)=\arccos(1-2c)/\pi\) for \(c\geq c_{\mathrm{GW}}\). s Then prove that for every edge \(i,j\), the probability that \(\mu'\) will cut the edge is at least \(g\left(\pE_\mu (x_i-x_j)^2\right)\).
References
Candès, Emmanuel J., Yonina C. Eldar, Thomas Strohmer, and Vladislav Voroninski. 2013. “Phase Retrieval via Matrix Completion.” SIAM J. Imaging Sciences 6 (1): 199–225.
Chan, Siu On, James R. Lee, Prasad Raghavendra, and David Steurer. 2013. “Approximate Constraint Satisfaction Requires Large LP Relaxations.” In FOCS, 350–59. IEEE Computer Society.
Cheeger, Jeff. 1970. “A Lower Bound for the Smallest Eigenvalue of the Laplacian.” In Problems in Analysis (Papers Dedicated to Salomon Bochner, 1969), 195–99. Princeton Univ. Press, Princeton, N. J.
Deza, Michel, and Monique Laurent. 1994. “Applications of Cut Polyhedra. I, II.” J. Comput. Appl. Math. 55 (2): 191–216, 217–47. doi:10.1016/0377-0427(94)90020-5.
Goemans, Michel X., and David P. Williamson. 1994.“879-Approximation Algorithms for MAX CUT and MAX 2SAT.” In STOC, 422–31. ACM.
Grothendieck, A. 1953. “Résumé de La Théorie Métrique Des Produits Tensoriels Topologiques.” Bol. Soc. Mat. São Paulo 8: 1–79.
Karp, Richard M. 1972. “Reducibility Among Combinatorial Problems.” In Complexity of Computer Computations, 85–103. The IBM Research Symposia Series. Plenum Press, New York.
Khot, Subhash. 2002. “On the Power of Unique 2-Prover 1-Round Games.” In STOC, 767–75. ACM.
O’Donnell, Ryan, and Yi Wu. 2008. “An Optimal Sdp Algorithm for Max-Cut, and Equally Optimal Long Code Tests.” In STOC, 335–44. ACM.
Raghavendra, Prasad, and David Steurer. 2010. “Graph Expansion and the Unique Games Conjecture.” In STOC, 755–64. ACM.
Trevisan, Luca. 2009. “Max Cut and the Smallest Eigenvalue.” In STOC, 263–72. ACM.
Waldspurger, Irène, Alexandre d’Aspremont, and Stéphane Mallat. 2015. “Phase Recovery, Maxcut and Complex Semidefinite Programming.” Math. Program. 149 (1-2): 47–81.